HEAT EXCHANGE OF BUILDING ⋆ Archi-Monarch

If you want to know about the cinemas design or climate and elements of climate or heat transfer in building, please click the link.

Heat exchange in a building refers to the transfer of heat between the building and its surroundings, which can have a significant impact on the building’s energy consumption and overall comfort level.

The building can be considered as a defined unit and its heat exchange processes with the out- door environment can be examined:

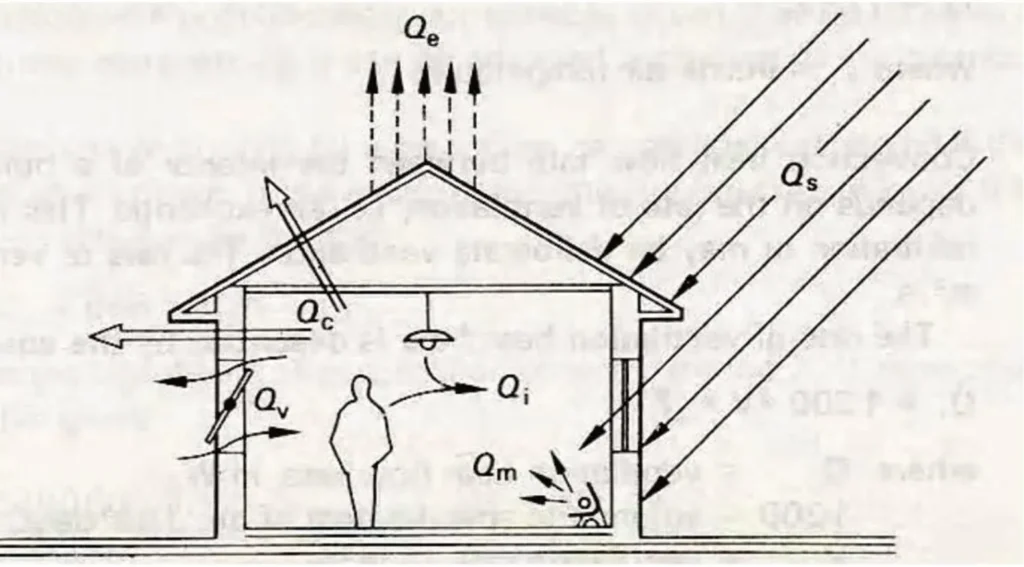
Q_i + Q_s± Q_c± Q_v± Q_m– Q_e= 0

Where,

Q_i = Internal heat gain
Q_s= Radiation through windows
Q_c= Heat gain or loss due to conduction
Q_v= Heat gain or loss due to covection
Q_m= Heat gain or loss due to mechanical equipment
Q_e= Heat loss due to evaporation

1) Conduction

Conduction of heat may occur through the walls either inwards or outwards, the rate of which will be denoted as Q_c (convective and radiant components in the transfer of the same heat at the surfaces are included in the term: transmittance)
Conduction heat flow through a wall of given area can be described by equation:

Q_c = A x U x _∆T

where

Q_c = conduction heat flow rate, in W
A = surface area, in m²
U = transmittance value, in W/m²degC
_∆T = temperature difference

The effects of solar radiation on opaque surfaces can be included in the above by using the sol-air temperature concept, but through transparent surfaces (windows) the solar heat gain must be considered separately. It may be denoted as Q_s

2) Radiation through windows

The effects of solar radiation through transparent surfaces (windows) the solar heat gain may be denoted as Q_s
If the intensity of solar radiation (I) incident on the plane of the window is known — this itself being a value denoting a density of energy flow rate (W/m²) — it will have to be multiplied by the area of the aperture only (m²) to get the heat flow rate in watts. This would be the heat flow rate through an unglazed
For glazed windows this value will be reduced by a solar gain factor (θ) which depends on the quality of the glass and on the angle of incidence.
The solar heat flow equation can therefore be established as:

Q_s = A x l x θ

where

A area of window, in m²
I = radiation heat flow density, in W/m²
θ = solar gain factor of window glass

3) Convection

Heat exchange in either direction may take place with the movement of air, e. ventilation, and the rate of this will be denoted as Q_v
Convection heat flow rate between the interior of a building and the open air, depends on the rate of ventilation, i.e., air exchange.
This may be unintentional air infiltration or may be deliberate ventilation, The rate of ventilation can be given in m³/s.:

The’ rate of ventilation heat flow is described by the equation: Q_v = 1300 x V x _∆T

Where

Q_v = ventilation heat flow rate, in W
1300 = volumetric specific heat of air, J/m³ degC
_∆T = temperature difference, deg C

If the number of air changes per hour (N) is given the ventilation rate can be found as: (3600 is the number of seconds in an hour)

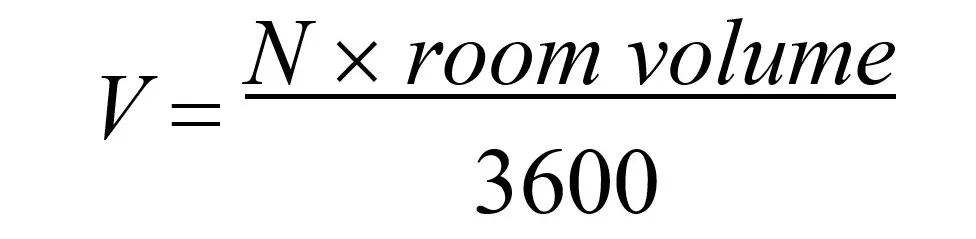
3) Internal heat gain

An internal heat gain Q_i may result from the heat output of human bodies, lamps, motors and
Heat output from a body (inside the building) is a heat gain for the building. Thus, the heat output rate appropriate to the activity must be selected and multiplied by the number of occupants. The result, in watts, will be a component of Q_i
The total rate of energy emission of electric lamps can be taken as internal heat gain. The larger part of this energy is emitted as heat (95% for incandescent lamps and 79% for fluorescent lamps) and the part emitted as light when incident on surfaces, will be converted into heat. Consequently, the total wattage of all lamps in the building (if and when in use) must be added to the Q_i
If an electric motor and the machine driven by it are both located (and operating) in the same space, the total wattage of the motor must be taken as Q_i .

4) Heating and cooling

There may be a deliberate introduction or removal of heat (heating or cooling), using some form of outside energy supply. The heat flow rate of such mechanical controls may be denoted as Q_m.
Heating and cooling, i.e., mechanical controls, the heat flow rate of these systems is subject to the designer’s intentions, and it is deliberately controllable.
It can thus be taken as a dependent variable in the equation, i.e., it can be adjusted according to the balance of the other factors.

5) Evaporation

Finally, if evaporation takes place on the surface of the building (e.g. a roof pool) or within the building (human sweat or water in a fountain) and the vapours are removed, this will produce a cooling effect, the rate of which will be denoted as Q_v
The rate of cooling by evaporation can only be calculated if the rate of evaporation itself is known. If the evaporation rate is expressed in kg/h, the corresponding heat loss rate can be found:

Qe = 666 x kg/h

As the latent heat of evaporation of water around 20°C is approximately 2400 kJ/kg, this gives: 2400000 J/h = 2400000/3600 J/s = 666W

The estimation of evaporation rate is a more difficult task, and it can rarely be done with any degree of accuracy (except under mechanically controlled conditions), as it depends on many variables, such as: available moisture, humidity of the air, temperature of the moisture itself and of the air and velocity of the air movement.
It can be measured indirectly, e.g., by measuring the reduction in the quantity of water in an open vessel, or it can be estimated from the number of people in the room, their activity and thus their likely sweat rate (a value between 20 g/h and 2 kg/h).
Usually, evaporation heat loss is either ignored for the purposes of calculations (except in mechanical installations), or it is handled qualitatively only: evaporative cooling will be utilized to reduce air temperature ‘as far as possible’.

To minimize heat exchange in a building, it is important to optimize the building’s insulation, ventilation, and shading. Insulation can reduce heat loss through the walls, roof, and floor, while ventilation can regulate the temperature and humidity of the indoor air. Shading can block the sun’s rays and reduce the amount of heat absorbed by the building.